Compreender o movimento vertical e a aceleração é fundamental para qualquer estudante que almeja um desempenho superior em provas e concursos.
Este estudo não só aprofunda o conhecimento em física, mas também estabelece bases sólidas para o entendimento de outros tópicos essenciais e avançados. Vamos desvendar os mistérios desse movimento e entender como ele se comporta sob diferentes condições.
O que você vai ler neste artigo
Movimento vertical
O movimento vertical pode ser facilmente observado no cotidiano. Um exemplo típico é quando deixamos cair um objeto. Este tipo de movimento é caracterizado por ser retilíneo e vertical, categorizado como um movimento uniformemente variado (MUV). A principal característica do MUV é a presença de uma aceleração constante que, nesse caso, é a aceleração da gravidade (g).
Aceleração da gravidade
Independentemente do objeto que se move em queda livre, no vácuo, todos irão experimentar a mesma aceleração devido à gravidade. Na superfície da Terra, essa aceleração é aproximadamente ( $$g = 10 , text{m/s}^2$$ ). Isto significa que, a cada segundo, a velocidade do objeto aumenta em 10 ( $$text{m/s}$$ ).
No entanto, na presença de ar, a resistência pode influenciar a queda, fazendo com que objetos mais leves, como uma pena, demorem mais para alcançar o chão em comparação a objetos mais pesados, como uma pedra.
Fórmulas e conceitos fundamentais
Para entender o comportamento de objetos em movimento vertical, utilizamos as seguintes equações derivadas do MUV:
- Equação da posição:
$$[ h(t) = h_0 + v_0 t – frac{1}{2} g t^2 ]$$
Onde:
- ( $$h(t)$$ ) é a posição do objeto em função do tempo,
- ( $$h_0$$ ) é a posição inicial,
- ( $$v_0$$ ) é a velocidade inicial,
- ( $$t$$ ) é o tempo,
- ( $$g$$ ) é a aceleração da gravidade.
- Velocidade em função do tempo:
$$[ v(t) = v_0 – g t ]$$
Onde:
- ( v(t) ) é a velocidade do objeto em função do tempo.
Essas fórmulas são modificadas dependendo da direção do movimento. Para o lançamento para cima, ( g ) é negativo porque a aceleração da gravidade está agindo contra o movimento. Para quedas livres ou lançamentos para baixo, ( g ) é positivo, pois a aceleração da gravidade age na mesma direção do movimento.
Aplicações práticas
Experimentos de queda livre
Uma maneira eficaz de visualizar essas fórmulas em ação é realizar experimentos de queda livre.
- Queda de uma Bola de Borracha: Se uma bola de borracha é solta de uma determinada altura, utilizamos a fórmula da posição para determinar quanto tempo a bola leva para atingir o solo.
- Lançamento Vertical de um Objeto: Imagine um aluno que lança uma bola para cima com uma velocidade inicial de 15 ( $$text{m/s}$$ ). Utilizando a equação da velocidade, podemos calcular o tempo até que a bola atinja o ponto mais alto (quando a velocidade é zero).
Tabela Resumo
| Variável | Descrição | Unidade |
|---|---|---|
| $$h(t)$$ | Altura em função do tempo | metros (m) |
| $$h_0$$ | Altura inicial | metros (m) |
| $$v(t)$$ | Velocidade em função do tempo | metros por segundo (m/s) |
| $$v_0$$ | Velocidade inicial | metros por segundo (m/s) |
| $$t$$ | Tempo | segundos (s) |
| $$g$$ | Aceleração da gravidade | metros por segundo ao quadrado (m/s²) |
Consequências para a preparação em provas
Entender a fundo o movimento vertical e a aceleração não só prepara os estudantes para resolver questões de física, mas também desenvolve um raciocínio lógico que pode ser aplicado em diversas áreas de estudo. Além disso, é um conhecimento fundamental para carreiras em Engenharia, Física, e outras Ciências Exatas.
Exercícios para praticar
Confira essa questão da UNIME:
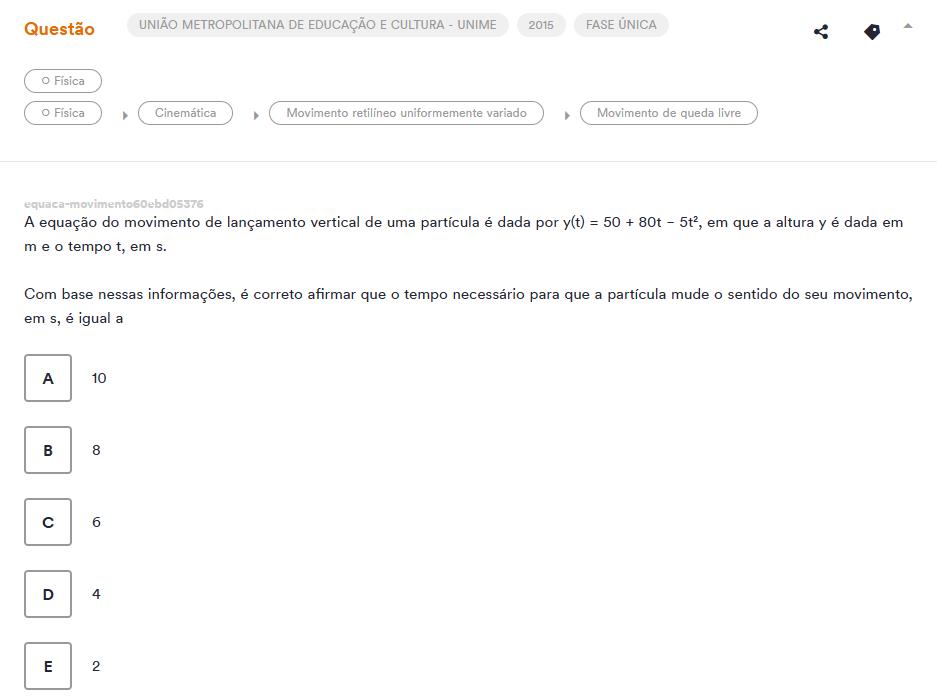
Alternativa correta: B
Confira essa questão da UECE:

Alternativa correta: D.
Para acessar a resolução completa, clique aqui.
Conclusão
O estudo do movimento vertical e da aceleração é uma pedra angular no curso de física. Compreender esses conceitos ajuda a construir um entendimento mais amplo e profundo de muitos outros fenômenos físicos. Este conhecimento é particularmente útil para estudantes que estão se preparando para grandes exames, como o ENEM ou vestibulares, oferecendo-lhes uma ferramenta valiosa para enfrentar e resolver problemas complexos.
O domínio das equações que governam o movimento vertical, a aplicação de conceitos práticos e a observação de experimentos são indispensáveis para um aprendizado eficaz. Portanto, dedicar-se ao estudo dessas áreas não só melhora o desempenho acadêmico, mas também prepara os estudantes para futuras etapas em suas jornadas educacionais e profissionais. Bons estudos e sucesso em todas as provas!
